Pertambahan dan Jarak

1.2 Pertambahan dan Jarak

Pertambahan

Gambar 1.9 memproduksi sebuah gambar yang dipotret secara berurutan (multiflash photograph) dari sebuah bola yang bergerak pada sebuah lintasan berbentuk lingkaran. Kisi-kisi koordnat pada gambar memberikan kita suatu cara untuk mengatakan dimana pusat-bolanya berada pada saat ketika bola dipotret.

          Ketika bola bergerak ke bawah dari B(19, 12) dan ke atas hingga C(39, 18), koordinat-x dari titik-pusat mulai bergerak dari x = 19 dan berhenti di x = 39 cm. Perubahan netto atau bersih  (dibaca "delta x") dalam koordinat-x adalah  = 39 - 19 = 20 cm. Koordinat-y berubah y = 12 cm hingga y = 18 cm, untuk suatu perubahan netto vertikal 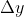 = 18 - 12 = 6 cm. Kita dapat berpikir bahwa  dan 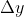 sebagai ukuran-ukuran dari perubahan netto horizontal dan vertikal.

Gambar 1.9

Sebuah reproduksi gambar yang dipotret secara beruntun dari sebuah bola yang bergerak melingkari sebuah lingkaran tegak. Bolanya dilepaskan dari keadaan diam di A(0, 32) dari ujung kiri teratas. Huruf-hurufnya memberi nama kedudukan-kedudukan yang berturutan. Koordinat-koordinat yang berikan adalah koordinatnya pusat bola, yang dibulatkan ke bilangan bulat terdekat. Sumbu-sumbu diskalakan dalam sentimeter.

CONTOH 1    Carilah perubahan-perubahan netto horisontal dan vertikal yang terjadi dalam kedudukan titik-pusat bola yang diperlihatkan dalam Gambar 1.9, apabila bola bergerak dari C(39. 18) hingga D(28, 18).

Pemecahan   Koordinat-x  berubah dari x = 39 cm menjadi x = 28 cm, untuk suatu perubahan netto

Koordinat-y mulai berangkat di y = 18 cm dan berakhir di y = 18 cm, untuk suatu bahan netto

Dalam matematika, perubahan-perubahan netto dalam koordinat-koordinat disebut pertambahan (increments). Apabila sebuah partikel bergerak dalam bidang dari sebuah titik awal  ke titik akhir , maka pertambahan-pertambahan  dan 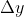 dalam koordinat-koordinat diberikan oleh rumus-rumus berikut :

  dan                   (1)

Untuk menghilangkan pertambahan dalam sebuah koordina, maka kita kurangi harga koordinat akhir dengan harga awalnya. Suatu pertambahan dapat berupa sembarang bilangan riel positif, negatif, dan nol. 

CONTOH 2  Gambar 1.10 memperlihakan lapisan partikel yang bergerak dari  = (1, -2) ke  = (6, 7). Pertambahan yang bersangkutan dalam koordinat-koordinat partikel yang dihitung dari Persamaan (1) adalah

   dan  

Gambar 1.10

Apabila sebuah partikel bergerak dari suatu titik ke titik lainnya, maka  dan 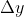 dihitung dari koordinat-koordinat kedudukan-kedudukan awal dan akhir. Apabila titiknya bergerak dari A ke B, maka perubahan netto koordinat adalah  dan  .

Jarak

     Apabila sumbu-sumbu koordinat dalam bidang mempergunakan suatu pengukuran yang sama, maka kita dapat menggunakan pertambahan-pertambahan koordinat yang digabungkan dengan teorema Pythagoras untuk menghitung jarak antara titik-titik dalam bidang.

Gambar 1.11 

Jarak dalam bidang koordinat dihitung dengan teorema Pythagoras.

      Memperlihatkan bagaimana caranya. Dalam menerapakan teorema Phythagoras untuk segitiga siku-siku , kita lihat bahwa jarak d antara dua buah titik  dan  diberikan oleh rumus berikut:

Persamaan (2) disebut rumus jarak untuk bidang.

CONTOH 3    Hitunglah jarak antara titik-titik (-1, 2) dan (2, -2).

Pemecahan    Jika kita mengambil  dan  maka , 

,                   
dan

Jika kita menamakan titik-titiknya terbaik, rumus dalam (2) tetap memberikan jarak antara mereka:

Pertambahan-pertambahan berubah tanda apabila kita menggunakan Persamaan (2) untuk menghitung jarak antara dua buah titik, maka tidaklah menjadi persoalan titik mana yang kita sebut  dan yang mana kita sebut .