Kemiringan dari sebuah Garis-Lurus
 Kemiringan dari Sebuah Garis-lurus
Kemiringan dari Sebuah Garis-lurus
Jika kita mengikuti perkembangan harga-harga makanan atau baja atau komputer, kita dapat mengamati perkembangan di atas kertas grafik dengan mengambari sejumlah titik dan mencocokan (fitting) titik-titik ini dengan sebuah kurva. Kita dapat memperluas kurvanya hari demi hari begitu muncul haraga-harga baru. Tetapi manfaat apakah yang dapat kita peroleh dengan membuat kurva demikian? Kita dapat melihat harga yang terdapat pada sebarang hari yang lampau. Kita dapat melihat dari kemiringan kurva (artinya yang tepat akan diberikan kemudian) laju perubahan pada mana harga-harga sedang naik maupun turun. Jika kita mengambari data-data yang lain pada lembar kertas grafik yang sama., maka kita mungkin dapat melihat hubungan yang dimiliki data-data yang baru ini dengan kenaikan dan penurunan harga-harga. Kurvanya dapat pula mengungkapkan pola-pola yang akan membantu kita untuk meramalkan masa depan dengan ketelitian yang lebih tinggi daripada seseorang yang tidak membuat grafik data-data ini,
Selain ini dari alasan-alasan dalam mana kalkulus terbukti sangat bermanfaat selama bertahun-tahun adalah bahwa subyek inimerupakan matematika yang tepat untuk membuat hubungan antara laju-laju perubahan dengan kemiringan-kemiringan dari kurva-kurva licin (smooth curves). Penjelasan mengenai hubungan ini merupakan salah satu sasaran dari pembahasan ini. Rencana dasarnya adalah pertama mendefinisikan apa yang kita magsudkan dengan kemiringan (slope) sebuah garis, dan kemudian mendefinisikan kemiringan-kemiringan sebuah kurva pada setiap titik di atas kurva sebagai kemiringan dari garis-singgung di titik-titik itu. Bagaimana ini dilakukan akan menjadi jelas begitu pembahasan ini berjalan. Langkah kita yang pertama adalah mencari suatu cara peraktis untuk menghitung kemiringan dari garis-garis.
Para insinyur sipil menghitung kemiringan dari sebuah alas-jalan (road bed) dengan menghitung perbandingan dari jarak yang ia naiki atau turuni terhadap jarak yang ia jalani secara horisontal. Mereka menyebut perbandingan ini gradien (grade) dari alas-jalan. Mereka biasanya menulis gradien-gradien dengan prosentase, seperti diperlihatkan dalam Gambar 1.14. Sepanjang pantai, gradien jalan kereta-api biassanya kurang dari pada gradien jalan-raya (highway) biasanya kurang dari pada 5%.
Dalam geometri-analitik kita definisikan kemiringan sebuah garis juga sebagai perbandingan dari tinggi (pertambahan vertikal, rise) terhadap maju (pertambahan horisontal, run) tetapi kita biasanya tidak menyatakan perbandingan-perbandingan ini sebagai prosentase.

Kemiringan
Untuk memulai, kita memisalkan L sebuah garis dalam bidang yang tidak sejajar sumbu-y. Misalkan) dan
dan ) dua buah titik sebarang pada L (lihat Gambar 1.15). Kita sebut
dua buah titik sebarang pada L (lihat Gambar 1.15). Kita sebut  sebagai tinggi dari
sebagai tinggi dari 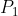 ke
ke 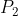 , dan
, dan  sebagai maju dari
sebagai maju dari 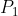 ke
ke 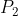 . Kenyataan bahwa L tidak vertikal mengatakan pada kita bahwa
. Kenyataan bahwa L tidak vertikal mengatakan pada kita bahwa  tidaklah nol. Kita definisikan kemiringan dari L sebagai tinggi per satuan maju. Jadi jika kita tunjukan kemiringan dengan m, maka kita peroleh yang berikut.
tidaklah nol. Kita definisikan kemiringan dari L sebagai tinggi per satuan maju. Jadi jika kita tunjukan kemiringan dengan m, maka kita peroleh yang berikut.




Untuk memulai, kita memisalkan L sebuah garis dalam bidang yang tidak sejajar sumbu-y. Misalkan



Andaikan bahwa daripada mmulih titik-titik 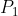 ke
ke 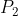 untuk menghitung kemiringan dalam Persamaan-(1), kita memilih suatu pasangan titik lainnya
untuk menghitung kemiringan dalam Persamaan-(1), kita memilih suatu pasangan titik lainnya  dan
dan  pada L dan menghitung
pada L dan menghitung
 (2)
(2)
Apakah kita akan memperoleh hasil yang sama untuk kemiringan? Dengan perkataan lain apakah
m' = m? Jawabanya ya, sebagaimana dapat kita lihat dari Gambar 1.16. Bilangan-bilangan m dan m' sama karena mereka adalah perbandingan-perbandingan dari sisi-sisi yang bersesuaian dari segitiga-segitiga yang sebangun:
 (3)
(3)
Kemiringan sebuah garis, sebagaimana telah kita mendefinisikannya hanyalah bergantung pada bagaimana curamnya garis tersebut menanjak atau menurun. Kita dapat menghitung kemiringan dari koordinat-koordinat dua buah titik-sembarang pada garis.
CONTOH 1 Hitunglah kemiringan garis yang melalui titik-titik ) dan
dan ) dalam Gambar 1.17.
dalam Gambar 1.17.
Pemecahan Kita pergunakan Persamaan (1) untuk memperoleh

Gambar 1.17 Kemiringan dari garis iniadalah m = (8-2)/(3-1) = 3. Ini berarti bahwa untuk setiap perubahan kedudukan pada garis.
untuk setiap perubahan kedudukan pada garis.
Pemecahan Kita pergunakan Persamaan (1) untuk memperoleh

Gambar 1.17 Kemiringan dari garis iniadalah m = (8-2)/(3-1) = 3. Ini berarti bahwa
Suatu kemiringan m = 3 berarti bahwa y bertambah 3 satuan setiap saat x bertambah 1 satuan. Dengan perkataan lain, perubahan dalam y adalah 3 kali perubahan dalam x. Sepanjang garis:  . Kemiringan m = 3adalah satuan faktor perbandingan.
. Kemiringan m = 3adalah satuan faktor perbandingan.
Andaikan kita mengambil 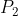 sebagai (1, 2) dari
sebagai (1, 2) dari 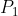 sebagai (3, 8) daripada yang sebaliknya. Apakah Persamaan (1) masih memberikan m = 3? Ya, seperti kita dapat lihat di sini:
sebagai (3, 8) daripada yang sebaliknya. Apakah Persamaan (1) masih memberikan m = 3? Ya, seperti kita dapat lihat di sini:
Menomori kembali titik-titik 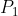 dan
dan 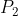 merubah tanda-tanda dari tinggi dan maju tetapi tidak merubah perbandingan mereka. Apabila kita pergunakan Persamaan (1) untuk menghitung kemiringan sebuah garis dari dua buah titik, maka menjadi masalah titik manakah yang kita ambilkan pertama dan yang kedua. Hal ini pada umumnya benar karena
merubah tanda-tanda dari tinggi dan maju tetapi tidak merubah perbandingan mereka. Apabila kita pergunakan Persamaan (1) untuk menghitung kemiringan sebuah garis dari dua buah titik, maka menjadi masalah titik manakah yang kita ambilkan pertama dan yang kedua. Hal ini pada umumnya benar karena
CONTOH 2 Hitunglah kemiringan dari garis yang melalui ) dan
dan ) dalam Gambar 1.18.
dalam Gambar 1.18.
Pemecahan Persamaan (1) memberikan
Kemiringan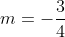 memberikan kita bahwa y berkurang 3 satuan apabila x bertambah 4 satuan.
memberikan kita bahwa y berkurang 3 satuan apabila x bertambah 4 satuan.
Pemecahan Persamaan (1) memberikan
Gambar 1.18 Kemiringan dari garis ini adalah (4-0)%3D-3/4) . Ini berarti bahwa y berkurang sebesar 3 satuan setiap x bertambah 4 satuan.
. Ini berarti bahwa y berkurang sebesar 3 satuan setiap x bertambah 4 satuan.
Kemiringan
Garis-garis yang menanjak bila x bertambah, seperti garis dalam Gambar 1.17, memiliki kemiringan-kemiringan positif. Garis-garis yang memenuhi bila x bertambah, seperti garis dalam Gambar 1.18, memiliki kemiringan-kemiringan negatif. Kemiringan dari setiap garis horisontal adalah 0. Sebuah garis horisontal tidak naik maupun terus. semua titik padanya memiliki koordinat-y yang sama, oleh karena itu tinggi  selalu 0.
selalu 0.





Comments
Post a Comment