Sudut-sudut Kemiringan

Sudut-sudut Kemiringan

Sudut-sudut kemiringan (angle of inclination) dari garis yang memotong sumbu-x adalah sudut positif yang dibuat garis itu dengan sumbu-x positif (Gambar 1.19). Sudut-kemiringan dari garis yang tidak memotong sumbu-x diambi berharga 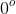 hingga tetapi tidak mengandung .

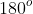Gambar 1.19

Sudut-sudut kemiringan diukur terhadap sumbu-x dalam arah berlawan perputaran jarum jam.

Contoh 3    Marilah kita perika kemiringan-kemiringan dari garis-garis yang sudut-sudutnya kemiringannya mendekati 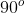, seperti

Gambar 1.20   Kemiringan sebuah garis adalah tangen dari sudut kemiringannya.

,          

dan

,           .

Kemiringan dari garsi-garis ini secara numerik sangatlah besar. Dengan mengambil 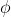 lebih mengambil  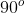kita dapat membuat kemiringannya secara numerik lebih besar daripada sebarang bilangan N, tidak peduli berapa besarnya N, kenyataan ini dapat diringkas dengan mengatakan bahwa kemiringan sebuah garis "menjadi tak-berharga" bila sudut-kemiringannya mendekati  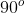atau bahwa sebuah garis vertikal memiliki "kemiringan yang tak-berharga". Tetapi, pada hakekatnya kita tidak menetapkan bilangan riel apapun sebagai kemiringan dari subah garis vertikal. Garis-garis vertikal tidak memiliki kemiringan.

Lambang untuk tak-berhingga adalah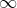 . Tetapi kita tidak boleh mempergunakan lambang ini dalam penjumlahan, pengurangan, perkalian dan pembagian seperti cara yang kita pergunakan dalam bilangan-bilangan dalam bilangan-bilangan biasa. Tak-berhingga bukanlah sebuah bilangan.