Lingkaran-lingkaran

Lingkaran-lingkaran

Persamaan untuk sebuah lingkaran dalam bidang koordinat adalah sebuah persamaan dalam x dan y yang dipenuhi oleh koordinat-koordinat titik-titik yang terletak pada lingkaran tetapi tidak dipenuhi oleh koordinat-koordinat sebarang titik lainnya.

     Persamaan standar untuk sebuah lingkaran dalam bidang diperoleh dari Persamaan (2) dengan cara berikut. Lingkaran yang jari-jarinya r satuan dan yang pusatnya terletak di titik (h, k) adalah himpunan dari semua titik dalam bidang yang jarak dari (h, k) adalah r satuan. Lihat Gambar 1.12(a). Dengan demikian, koordinat-koordinat dari sebarang titik P(x, y) pada lingkaran ini memenuhi persamaan

atau, jika kta kuadratkan kedua belah ruas,

Sebaliknya, sebarang titik dalam bidang yang koordinat-koordinatnya memenuhi

Gambar 1.12     (a) Untuk titik-titik P(x, y) pada lingkaran berjari-jari r yang berpusat di (h, k), 

.   Untuk titik-titik P(x, y) pada lingkaran berjari-jari r yang berousat di titik asal, .
Persamaan (3) adalah sebuah titik yang jaraknya ke titik (h, k) adalah r satuan. Singkatnya, Persamaan (3) adalah sebuah persamaan untuk lingkaran.

Jika pusat lingkaran berada di titik-asal, maka h dan k dalam Persamaan (3) kedua-duanya dengan 0 dan persamaan (3) menjadi . (Lihat Gambar 1.12b)


CONTOH 4     Tuliskan sebuah persamaan untuk lingkaran yang berjari-jarinya 7 sauan dan pusatnya di titik (2, -3).

Pemecahan      Kita ambilkan h = 2, k = 3, dan r = 7 dalam persamaan (3) dan memperoleh

Karena tidak ada alasan khusus untuk menguraikan kuadrat dari suku-suku di sebelah kiri, maka persamaan ini adalah yang kita cari.

   CATATAN     Rumus jarak   dalam persamaan (2) menghitung d dalam satuan apapun dalam mana kedua sumbu diskalakan. Sebagai misal, andaikan x dan y diberikan dalam meter. Maka pertambahan-pertambahan ,  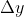adalah dalam meter, kuadratnya dalam meter kuadrat, jumlah kuadrat-kuadratnya dalam meter kuadrat, dan akar pangkat dua dari jumlah ini dalam meter lagi.